Javascript Draw Points Around Circle

Processing is a powerful generative art library available in a number of languages including Java, JavaScript, Android, and iOS. Circles and ellipses are among the many geometric functions processing afford artists. They are specially useful in helping to place items in an evenly distributed manner.

1. 1 Quick Trigonometry Refresher
2. 2 Step 1: Draw a Reference Circle
3. three Step 2: Draw a Point on the Circle
4. 4 Step 3: Adding an First
5. five Stride 4: Adding Multiple Points
6. 6 Getting Creative
7. 7 Terminal Thoughts

This tutorial will walk through the process of creating a circle to be used equally a guide for spacing objects evenly. We will use a bit of trigonometry and a scattering of P5JS's handy functions. By the finish—we'll be creating a circle onto which we tin evenly space any number of objects we choose!

Quick Trigonometry Refresher

We don't need much math to make this magic happen but some basic trigonometric knowledge is a must. Specifically, we need to know how to find a point on a circumvolve given the radius, angle, and in our instance; the relative position of the circle'south origin. This means we need to find the x-coordinate and y-coordinate. The formula for these points—using the unit of measurement circle—are as follows:

A signal on a circumvolve is institute using an angle and the sin and cos function.

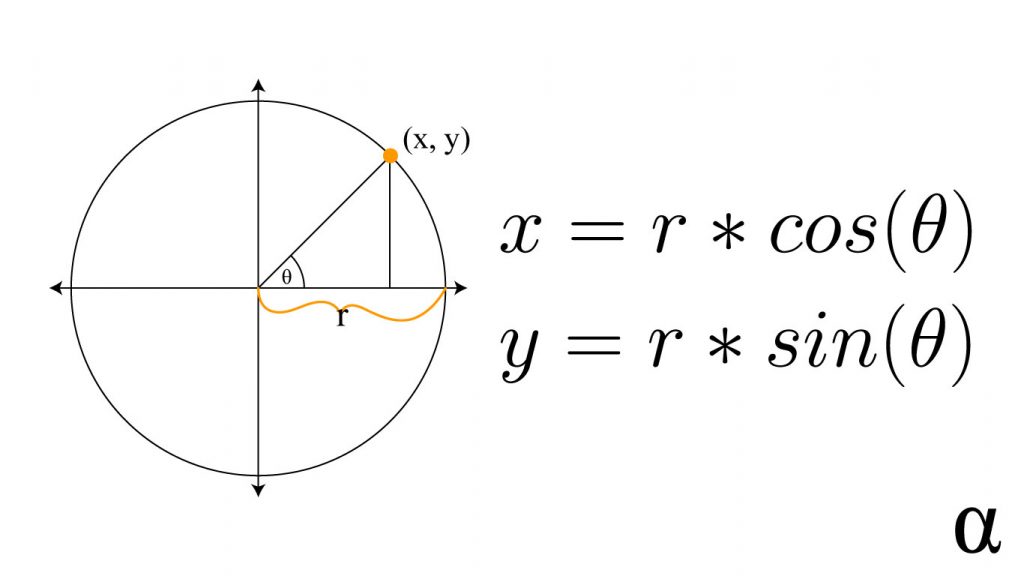
These are the functions we volition implement using P5JS to get a indicate on our circle. Past using angles that are fractions of 2*PI (a.k.a. 360 degrees) we can decide how much space a point on our circle should have between itself and the neighboring points. Enough chatter—let's start coding!

Footstep 1: Describe a Reference Circle

The showtime footstep is to draw a circle on which our points will be placed. P5JS offers two main means of achieving this. The first, using the built-in circle method, is the most straightforward arroyo. Alternatively, we could use the ellipse office but there is no particular need in this case. Create a circle with the following lawmaking:

/**  * Initialization function by P5JS  */ function setup(){          // Creates the HTML sail object to which all     // drawing is projected.     createCanvas(1360, 768)          // Fills the canvas object with a background color     background("#efefef") }  /**  * Primary update function called each frame by P5JS  */ part draw(){          // Define styles of our geometry (circle)     stroke('blackness')     strokeWeight(15)     noFill()          // Create the circle     circle(width / 2, height / 2, 512) }

In this script, we've created a canvas object of size 1360px x 768px, added a background color, and created a circle object with a black stroke color and no fill. Hither'south the paradigm, that will serve as our jumping-off point:

A simple circle, fatigued using P5JS'due south built-in circle() function.

Step two: Draw a Point on the Circle

Nosotros demand to outset draw a single point on our circle before we starting time loading this circle upwards with lots of points. This can exist achieved by applying the two formulas from above with the post-obit lawmaking in our draw() function just after we've fatigued the circumvolve:

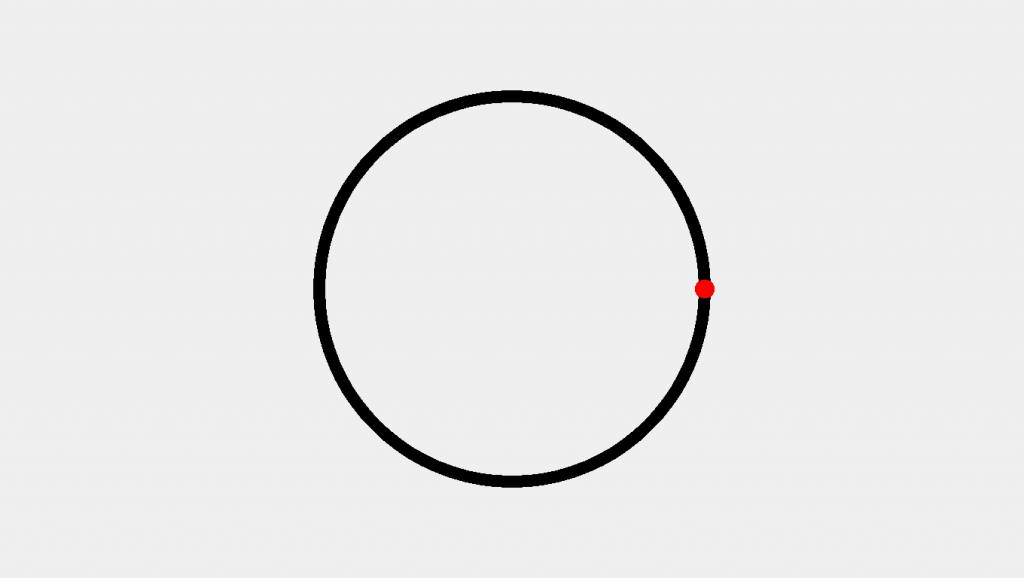
// Depict a single point allow bending = 0; let x = bore / ii * Math.cos(bending); allow y = diameter / 2 * Math.sin(angle) stroke('crimson') strokeWeight(25) point(10, y)

In this block we've created a new variable for the angle we'll use for calculation. In math class, you'll hear this called theta (Θ). We've also created two variables x, y to make the calculations more clear for our angles. Later that, nosotros've told P5JS we want the indicate to be crimson and of size (strokeWeight) 25. This results in the following image:

Here we see our circle having been created, though it appears to exist incorrectly placed. (upper left)

Yikes. We've created a point all correct but it doesn't seem to be where nosotros wanted it. So what gives—were our calculations wrong?

Stride 3: Adding an Get-go

The issue is that when using unit circle trigonometry one assumes the origin (centre point of the circle) is at the ten,y coordinates (0, 0). Ours is located at 680 (width / 2), 383 (height / 2). To gear up this, we need to relocate our point or origin as shown in the following image:

We demand to account for starting our calculation at the middle of our circle instead of the sheet center.

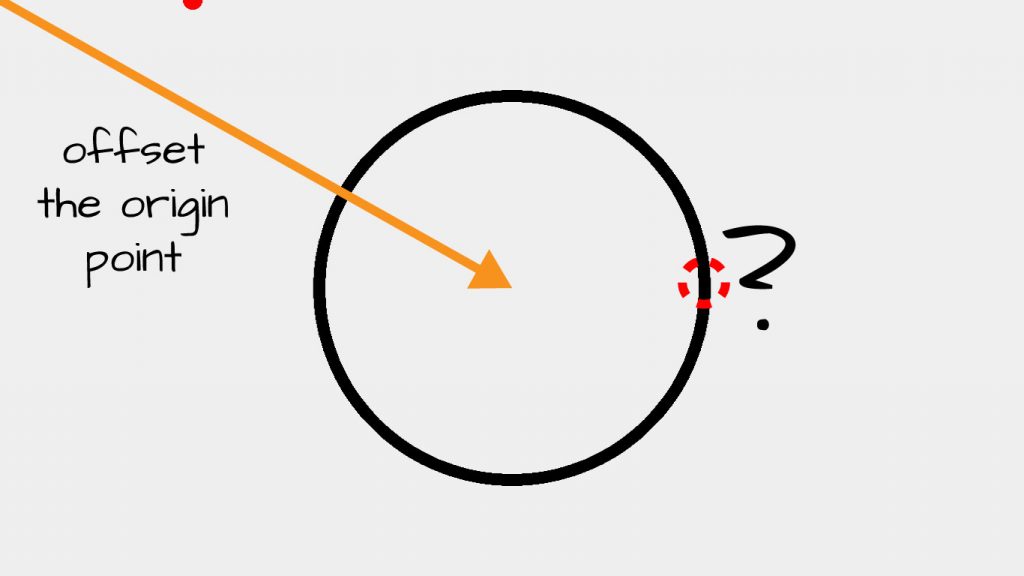
This is an issue considering P5JS uses a coordinate organisation where the upper-left of the canvas is the origin. See here for a more in-depth word. To remedy this situation nosotros need only add together a elementary offset to our equations past updating our code in the following way:

// Utilize trigonometric functions to calculate a indicate // on the circumvolve and calculation an showtime to account // for the position of our circle's middle. let x = diameter / 2 * Math.cos(angle) + width / 2; let y = diameter / ii * Math.sin(angle) + tiptop / 2;

Annotation we've added calculated values of width/2 and height/2 for our circle's center coordinates. These are P5JS built-in keywords that return both the width and height of the canvass object we created in the showtime pace. This makes our trigonometric functions relevant to the center of our circle rather than the world (0, 0) coordinates that happen to be at the elevation-left corner of the canvas object. This tweak produces the following prototype:

The betoken is at present located on the border of our circle, having been offset accordingly.

Stride 4: Adding Multiple Points

Now that nosotros have figured out how to add a point to our curve we can begin conceiving of how to add together multiple points. We are going to approach this problem iteratively, adding a serial of points one afterwards some other. Even so, we need to increment our angle during each iteration to ensure our points aren't overlapping. We'll approach this with the post-obit update to our draw() function:

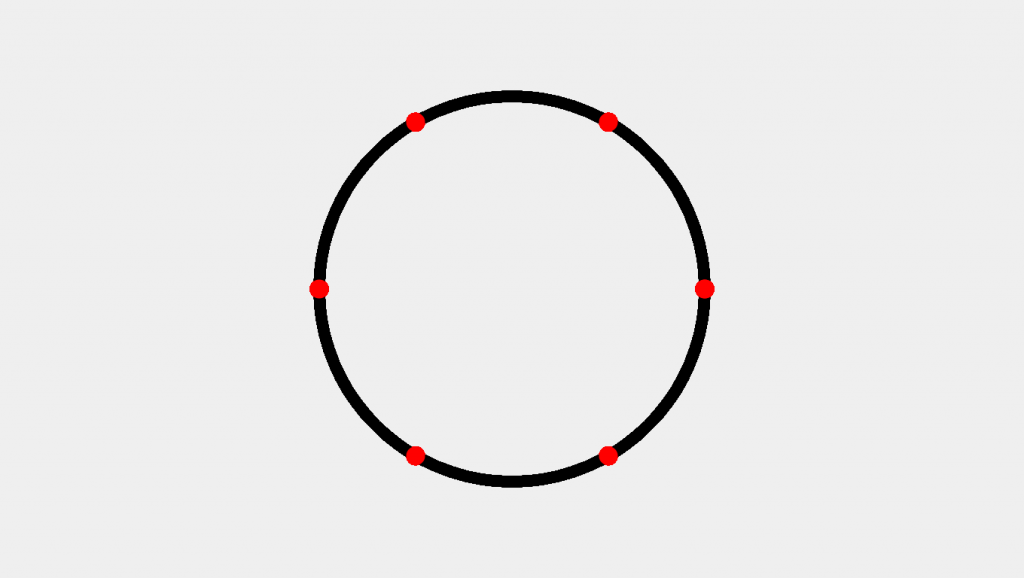
// Create and initialize a variable for the  // Number of points to be drawn on our circle let pointCount = 6;  // Create and initialize a variable from which // we will start drawing points. let bending = 0;  // Iteratively describe points incrementing by 360 / pointCount for(let i = angle; i < 360 + angle; i+=360 / pointCount){     let x = diameter / 2 * Math.cos(i) + width / 2;     let y = diameter / 2 * Math.sin(i) + height / ii;     point(10, y) }

Here we've used an iterator i set to an initial value of angle which loops in increments of 360 / pointCount until reaching a value of 360 + bending. The + angle component ensures that if we start our angle at a not-nil value we will continue to increase until the get-go angle is reached. Let'south meet the result:

Here nosotros take the correct number of points merely the spacing is wrong.

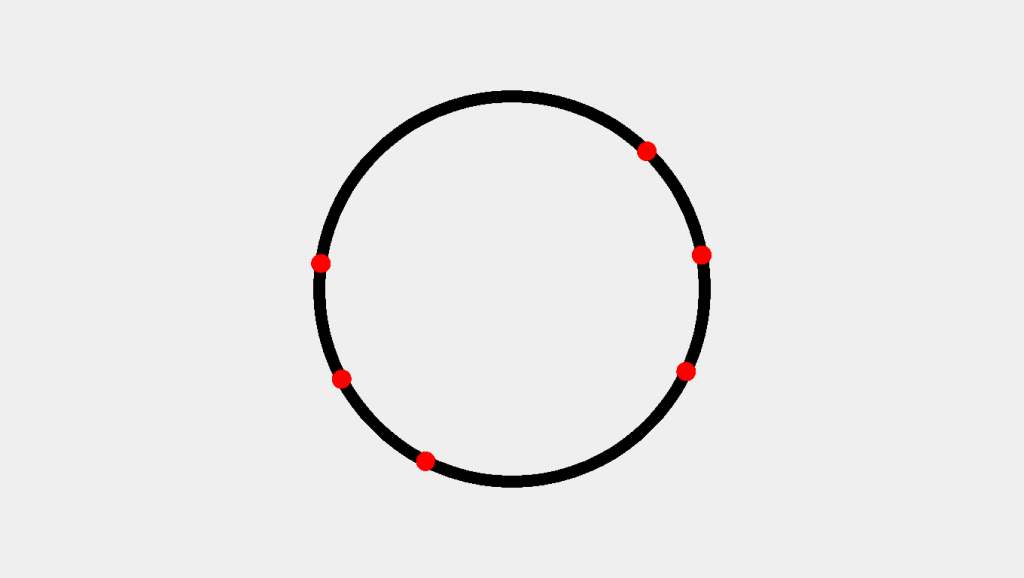
Yikes. Here we've created the correct number of points. In that location also seems to besomecourse of spacing going on—but certainly not anevenly distributed spacing. The consequence is that we are using 360—a value in degrees—when P5JS expects a value inradians past default. We can remedy this past using one of two post-obit adjustments;

1. Using the radians() function to catechumen the values of degrees;
2. Using a congenital-in value of PI (P5JS'southward PI or JavaScripts Math.PI);

The Unit of measurement Circumvolve presents values calculated in terms of radians. Equally such, near trigonometric functions use radians by default. Fortunately, any language worth its table salt provides built-in methods to catechumen radians to degrees or hands use values of PI. Cheque out this video past Khan Academy for more data on Radians vs. Degrees.

Below illustrates both a PI-relative approach and a degrees-to-radians approach

/////////////////////////////////////////////////////////////////// //// Radian Conversion Approach  // Supersede Angle with PI let bending = PI;  // 0 would withal work here let pointCount = 6;  // Update 360 to TWO_PI, however offset via angle for(allow i = angle; i < TWO_PI + angle; i += TWO_PI / pointCount){     let x = diameter / 2 * Math.cos(i) + width / two;     let y = diameter / 2 * Math.sin(i) + height / 2;     point(x, y) }  /////////////////////////////////////////////////////////////////// //// Radian Conversion Approach  // Create a circle with angles converted from degrees let angle = 0; let pointCount = 6; for(permit i = angle; i < radians(360 + angle) ; i += radians(360 / pointCount) ){     let 10 = diameter / 2 * Math.cos(i) + width / 2;     let y = bore / two * Math.sin(i) + height / 2;     indicate(x, y) }

Here we run across both approaches—using P5JS's TWO_PI (equivalent to PI * 2 or Math.PI * two) as well as the radians(360 / pointCount) approach. Whichever approach we might choose, the following epitome will be produced:

A circumvolve with 6 evenly-spaced points, located along the border.

Getting Creative

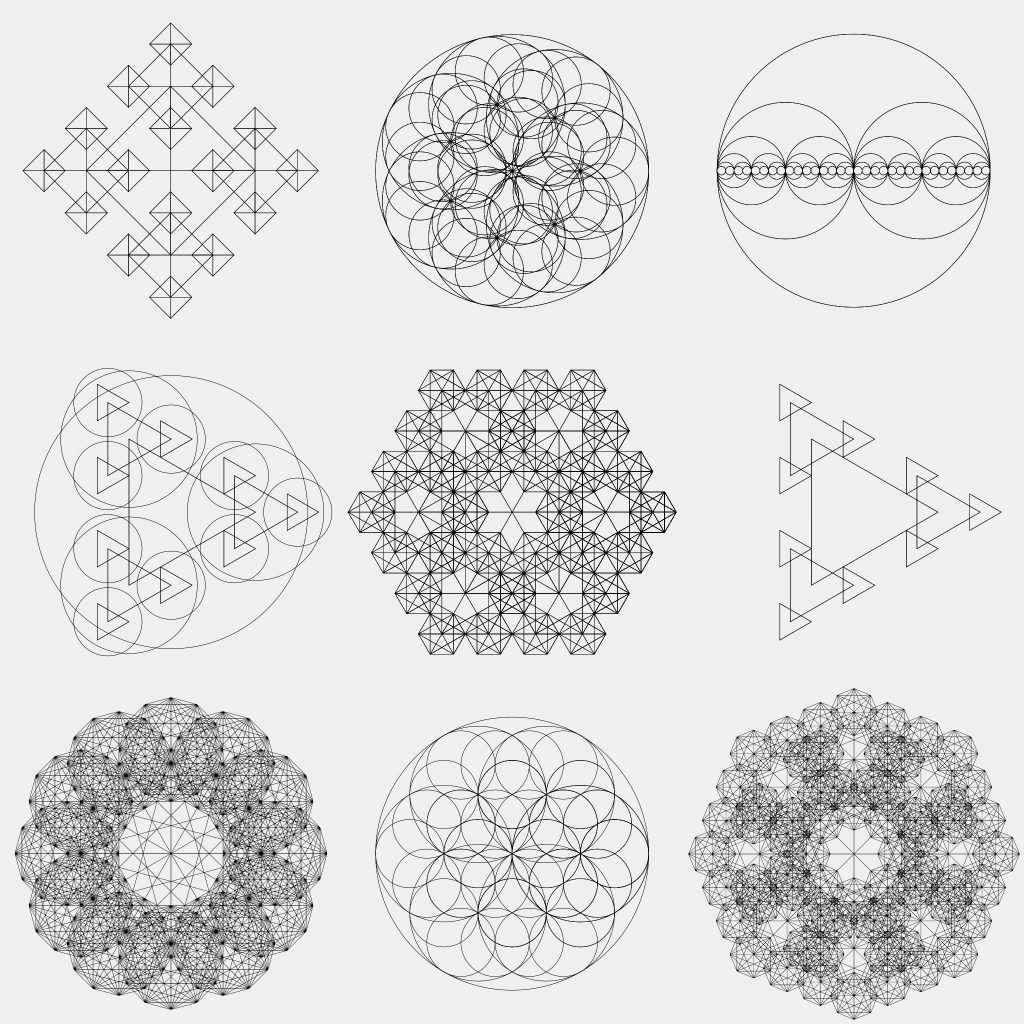
Locating points forth a circle tin requite rise to all sorts of possibilities. One tin can apply them to create irregular filigree designs, influence menstruation fields, or but encounter what type of patterns one can generate past fiddling around with the radius, signal spacing, and visualizing those connections. Below is a grid of images created using points spaced evenly along a curve to directly the output of a recursive algorithm:

A grid of patterns created using evenly spaced points most circles to locate the origin signal of a recursive function. (click to overstate)

Terminal Thoughts

P5JS (and Processing generally) is a powerful visualization tool. Mastering fundamental operations, such as spacing objects evenly forth a circle'due south border, tin help build a robust toolkit by which one can create mesmerizing generative art. The positions of these dots—besides as the circumvolve—tin serve equally placements for other objects.

Calculation in unique combinations of offsets, random variance, color, size, shape, etc. tin can build to create truly circuitous artwork. And to call up—all this is possible because we figured out how to evenly space a few points forth the border of a circle! If y'all're looking for more than fundamentals check out the article on how to describe a squiggly line in P5JS!

brunkercollow.blogspot.com

Source: https://www.alpharithms.com/evenly-spacing-objects-around-a-circle-in-p5js-processing-180222/

Share :